A Computer Science Proof Of Why Nice Guys Do Not Finish Last (But First).
4 Eye-Opening Insights On Playing & Winning The Game Of Your Life
Have you heard the quote — “Nice guys finish last”?
This story is about using some mathematics and computer science to figure out if this is true or not.
Let’s begin by learning a bit about Game Theory.
What Is Game Theory?
Game theory is a branch of mathematics that studies strategic decision-making in situations where multiple rational players interact, and the outcome for each player depends on the actions of all participants.
The decision-makers in the interaction (Game) are called Players and they use different actions (Strategies) to gain a reward (Payoff).
A ‘Rational’ player is one who makes decisions intending to maximise their returns.
Game theory is extensively used to study the behaviour of different players in fields like Economics, Political Science, Law, Biology, Computer Science, and more.
Questions like the following can be addressed using the theory —
How can nations make decisions without conflicts?
Why do inherently selfish individuals start cooperating in a population?
Are out-of-court settlements better than in-court ones?
Many interactions/ games have been studied using Game theory but the Prisoner’s Dilemma is one of the most famous ones.
Let’s learn about it next.
What is the Prisoner’s Dilemma?
The Prisoner’s Dilemma is a thought experiment in Game theory that involves two suspects (players) who have been arrested for a crime.
The police keep each of them in a separate room and offer them a deal.
The deal is as follows —
If both suspects confess to the crime/ defect, they will each serve 2 years in prison.
If one suspect confesses/ defects while the other remains silent/ cooperates, the confessor will be released, and the silent suspect will serve 3 years in prison.
If both suspects remain silent/ cooperate, they will each serve only 1 year in prison.
The different situations can be represented using a payoff matrix as shown below.
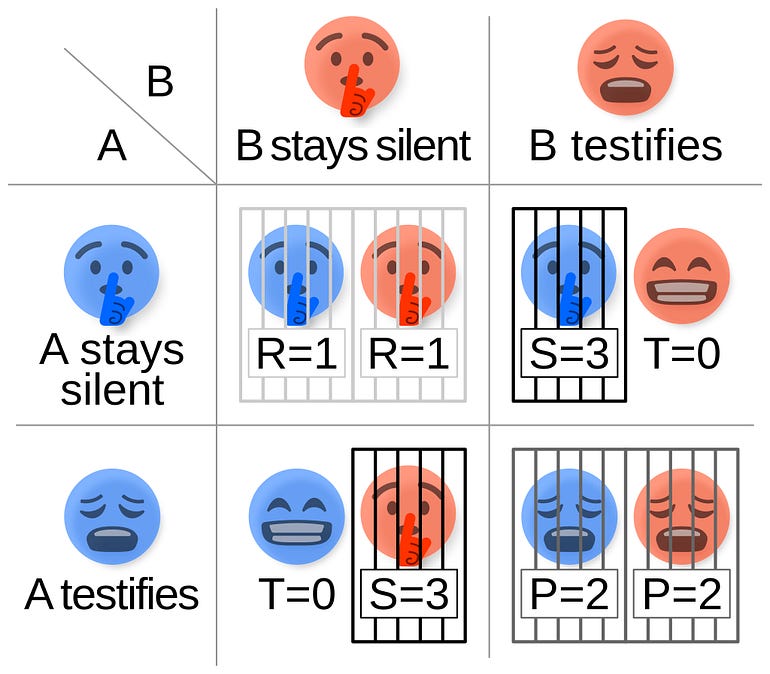
It looks as if defecting/ betraying the other suspect is the better choice at an individual level (as it leads to just 1 year in prison).
But, if both of the suspects follow the same reasoning, they both end up in prison for 2 years.
Thus, the Prisoner’s Dilemma highlights that decisions made in self-interest can lead to poor outcomes for all involved players and that cooperation is the best strategy in such cases.
Let’s move to the next step to understand the Iterated Prisoner’s Dilemma.
What Is The Iterated Prisoner’s Dilemma?
It is an extension of Prisoner’s Dilemma where the game is played repeatedly by the same players and each gets an opportunity to learn from their past actions and to establish a reputation.
Iterated Prisoner’s Dilemma has been extensively studied over the years and one such example of an experiment is Prof. Robert Axelrod’s tournament.
More On Axelrod’s Tournament
Prof. Robert Axelrod, a political scientist at the University of Michigan, conducted a famous experiment in 1980 that was based on the Iterated Prisoner’s Dilemma.
He invited the world’s smartest minds from different fields and asked them to submit computer programs that would play against each other in a computer tournament based on their strategy of choice.
The tournament was structured so that each strategy would play against every other strategy, including itself, for 200 rounds of the Prisoner’s Dilemma.
The rewards would be as follows —
Cooperation scores 3 points each
Mutual deflection scores 1 point each
If one player cooperated while the other defected, the defector scored 5 points, and the cooperator scored 0 points.
The goal of each strategy was to score as many points as possible during this tournament.
To ensure legitimate results, the tournament was repeated 5 times over.
There was a total of 15 strategies that were submitted and these entries came from 3 countries and the experts of 5 disciplines.
These were some of the submitted strategies —
Tit for tat: A player starts by cooperating and then mimics the previous action of the opponent.
Friedman: A player starts by cooperating however will defect all along if at any point the opponent has defected.
Grofman: If the players did different things on the previous move, this player cooperates with a probability of
2/7. Else, it always cooperates.Joss: A player cooperates 90% of the time after cooperation by the other player but always defects after a defection by the other.
Random: A player who randomly chooses between cooperating and defecting
Note that some of these strategies are more cooperative or ‘nice’, while others are more defective or ‘bad’.
Similarly, some strategies have simple-to-follow rules while others use extremely complex algorithms to decide their next move.
The Tournament Begins
As the battle between the strategies began, many believed that the sneaky and algorithmically complex strategies would have the upper hand over the others.
Instead, the results were quite the opposite (and shocking)!
The results were as shown in the table below.
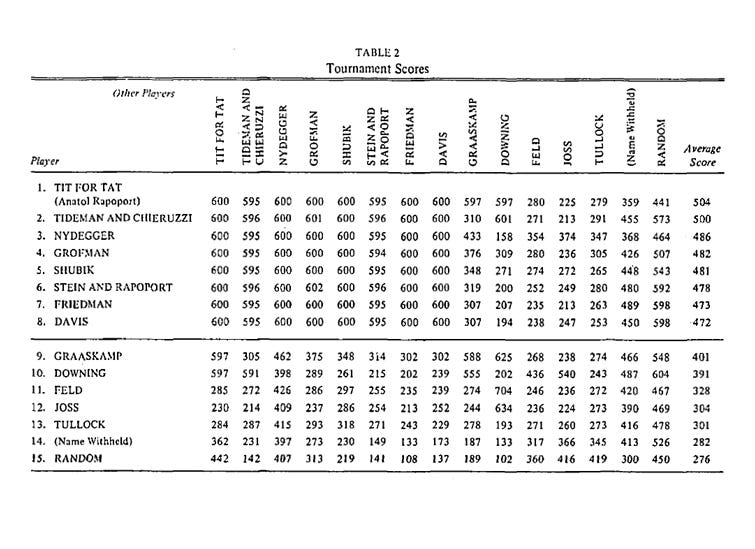
The winner of the tournament was the simplest strategy called—
Tit For Tat.
It scored 504 out of a total of 600, the best score that could be obtained if both sides continually cooperated.
Surprising Life Lessons From The Tournament
The tournament’s results highlighted some really important insights that will completely change your perspective on how to play the ‘game’ of life.
These findings are as follows —
1. Forgiveness Is Powerful
A strategy was called more forgiving if it still cooperated in the moves after the other player had defected.
For example, Tit for Tat, a strategy that did not hold a grudge and just acted according to the last move of its opponent.
It was seen that the winning strategies were more forgiving than the losing ones.
2. Simplicity Rules Over Complexity
The simplest of all strategies, Tit for Tat, was written in only four lines of code in FORTRAN, and it scored the highest (504 points).
On the other hand, the strategy ‘Name Withheld’, a 77-line program written by a graduate student of political science whose dissertation was in game theory, ended up in 14th place in the tournament with a score of 282.
This shows that the simpler strategies ruled over the complex ones.
3. Always Consider Your Surroundings
There were two strategies in particular in the tournament that influenced the relative rankings of the top-performing strategies.
These were Graaskamp and Downing, and they were called ‘Kingmakers’.
The top strategies’ success was largely determined by how well they performed against the kingmakers.
This finding is quite interesting and shows how the ability to handle and adapt to unpredictability created by the ‘Kingmakers’ determined the success of other strategies.
This shows how important it is to consider your surroundings and adapt to them to thrive.
4. Niceness Leads To Better Outcomes
All of the top 8 ranking entries are nice while none of the other entries are nice.
The worst-performing ‘nice’ strategy called ‘Davis’ scored 472, which is still 71 points ahead of the best-performing ‘bad’ strategy called ‘Graaskamp’, which scored 401.
In simpler words, if a strategy was not the first to defect, it was overall more successful!
Moving on to the conclusion —
Yes, Nice Guys Do Finish First! (Q.E.D.)

References
Original research publication titled ‘Effective Choice in the Prisoner’s Dilemma by Prof. Robert Axelrod’
What Game Theory Reveals About Life, The Universe, and Everything by Veritasium on Youtube
Run the results yourself using the Axelrod Python library
Introducing Game Theory: A Graphic Guide by Ivan Pastine, Tuvana Pastine and Tom Humberstone


